Radianes y Gradianes: noviembre 2011

RADIANES Y GRADIANES

http://www.google.com.co/#sclient=psy-ab&hl=es&source=hp&q=radianes+y+gradianes&pbx=1&oq=radianes+y+gradianes&aq=f&aqi=&aql=&gs_sm=e&gs_upl=48008l51633l0l51759l20l16l0l1l1l4l1717l7550l2-1.3.5.4.8-1l15l0&bav=on.2,or.r_gc.r_pw.,cf.osb&fp=f56e01a655d37e2a&biw=1280&bih=656

http://es.wikipedia.org/wiki/Radi%C3%A1n

Como se hace la conversion de gradianes a radianes y veceversa?

gradianes son los grados centesimales, y resultan de dividir un ángulo recto en cien unidades

1 de circunferencia tiene:

=400 gradianes (tambien llamados centsimales)
=360 grados sexagesimales
=2π radianes

Si quieres pasar de uno a otro aplica regla de 3:

De Radianes a Gradianes:
-------------------------------------

2π radianes............400 gradianes
X rad...............cantidad gradianes

X radianes=(cant gradianes)(2π radianes)/400 gradianes

Es decir:

X radianes=cantidad*π/200

Donde cantidad es una cantidad tuya conocida, la cantidad de gradianes que quieres pasar a radianes.

De Gradianes a Radianes:
-------------------------------------

Analogamente al anterior:

2π radianes............400 gradianes
cantidad rad..............X gradianes

X gradianes=(cant radianes)(400 gradianes)/2π radianes

Es decir:

X gradianes=cantidad*200/π

X termina expresado en gradianes
Donde "cantidad" es una cantidad tuya conocida, la cantidad de radianes que quieres pasar a gradianes

gradianes

El grado centesimal o gradián (plural: gradianes), originalmente denominado gon, grade o centígrado —nombres aún en uso en otros idiomas, por ejemplo en portugués se escribe grado— resulta de dividir un ángulo recto en cien unidades. La circunferencia se divide, así, en 400 grados centesimales. Un grado centesimal equivale a nueve décimos de grado sexagesimal. En las calculadoras suele usarse la abreviatura grad. Se representa como una "g" minúscula en superíndice colocada tras la cifra. Por ejemplo: 12,4574g

Radianes

El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es rad.

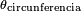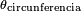El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios; es decir, θ = s /r, donde θes ángulo, s es la longitud del arco, y r es el radio. Por tanto, el ángulo completo, $\scriptstyle{\theta}_\text{circunferencia}$ , que sustiende una circunferencia de radio r, medido en radianes, es:

$\theta_\text{circunferencia}=\frac {L_\text{circunferencia}}{r} =\frac {2 \pi r}{r}=2 \pi\ \text{rad}\,$

lunes, 21 de noviembre de 2011